Understanding LoRA: Efficient Fine-Tuning

In the world of Large Language Models (LLMs) and generative AI, fine-tuning has traditionally been a resource-intensive process. Retraining a model with billions of parameters requires massive computational power and GPU memory. Enter LoRA (Low-Rank Adaptation), a technique that has revolutionized how we adapt these models to specific tasks.

What is LoRA?

LoRA, or Low-Rank Adaptation, is a parameter-efficient fine-tuning technique introduced by Microsoft researchers in 2021. Instead of updating all the weights of a pre-trained model, LoRA freezes the original model weights and injects pairs of rank-decomposition matrices into the layers of the Transformer architecture.

How It Works

The core insight behind LoRA is that the change in weights during model adaptation often has a low "intrinsic rank". This means that while the model itself resides in a high-dimensional space, the updates needed for a specific task can be represented effectively in a much lower-dimensional space.

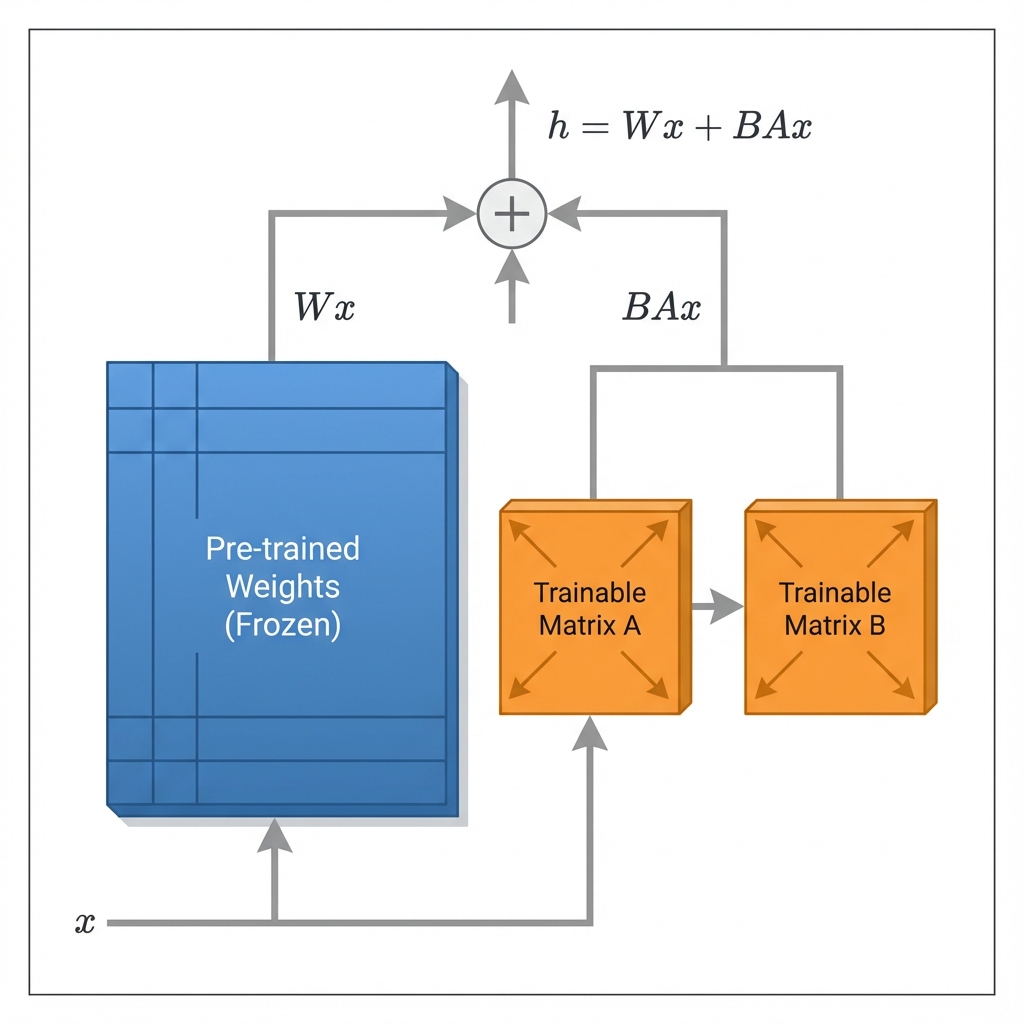
1. Freezing Weights: The original pre-trained weights ($W$) are frozen and not updated during training.
2. Injected Matrices: Two small matrices ($A$ and $B$) are added to the layer. The update $\Delta W$ is represented as $B \times A$.
3. Forward Pass: During inference, the output is computed using both the original weights and the adapter weights: $h = Wx + BAx$.

Key Benefits

• Efficiency: LoRA reduces the number of trainable parameters by up to 10,000 times and GPU memory requirements by 3x.
• No Latency Penalty: Since the trained matrices can be merged with the original weights during deployment, there is no additional inference latency.
• Storage: Instead of saving a full copy of the fine-tuned model (often gigabytes), you only need to store the small LoRA matrices (often megabytes).
• Modularity: You can switch between different tasks by simply swapping out the LoRA adapters while keeping the base model loaded.

When fine-tuning a model, previously one had to rely on Supervised Fine-Tuning (SFT), which is essentially having to retrain an existing model, which is expensive in terms of energy and time.

In the early days of machine learning, it was feasible to build a model and train it in a single pass. But with the explosion of more specific, tailored use cases, there are two stages: pre-training and then fine-tuning. Generally, a large data set is used for the initial pass and then a follow up fine tuning on a smaller, refined dataset is used to calibrate it.

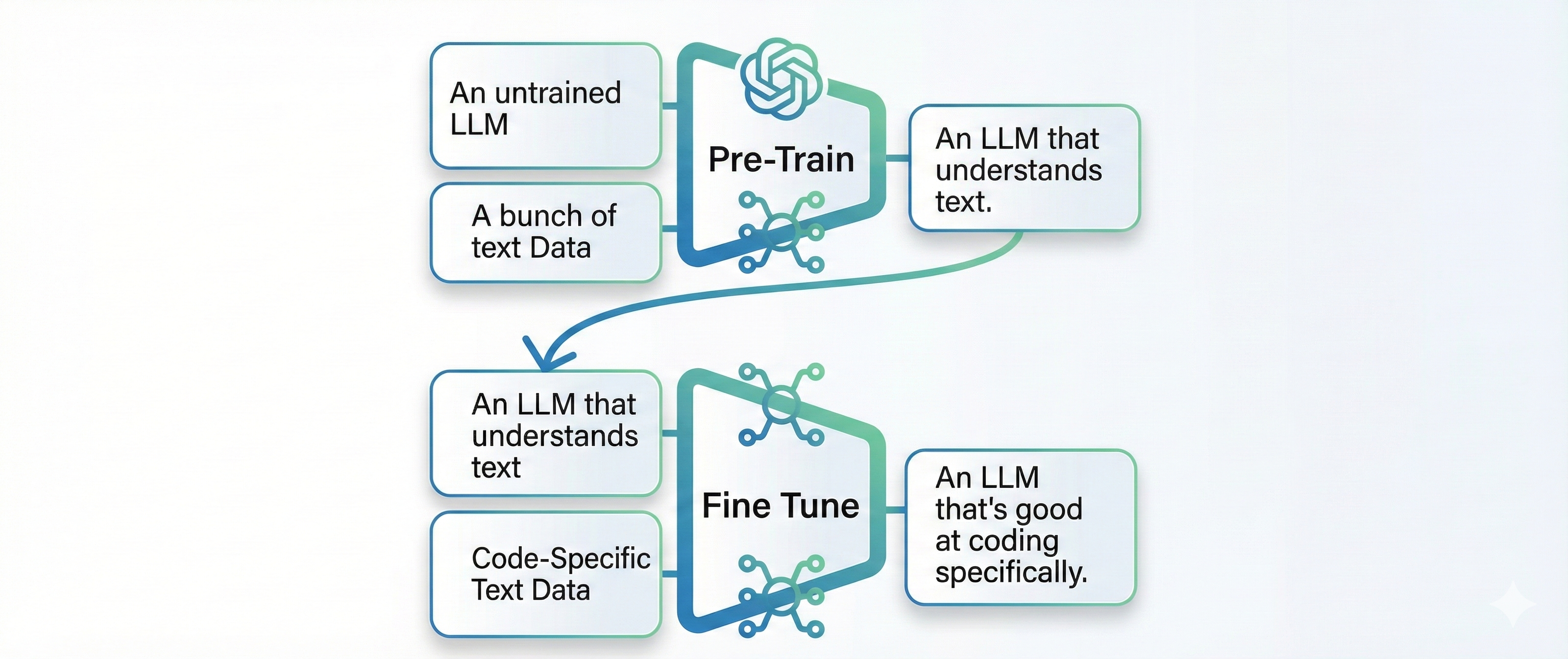
However, there are some barriers in fine-tuning. This strategy is expensive since LLMs are extremely large. To fine tune using this strategy would require enough memory to not only store the entire model, but also gradients for every parameter in the entire model. Gradients are used to inform how a small change in a certain parameter will impact model output. In back propagation, a prediction is created, gradients are calculated, the loss function is used to determine how far off the result is, then the gradients are used to improve the parameters.

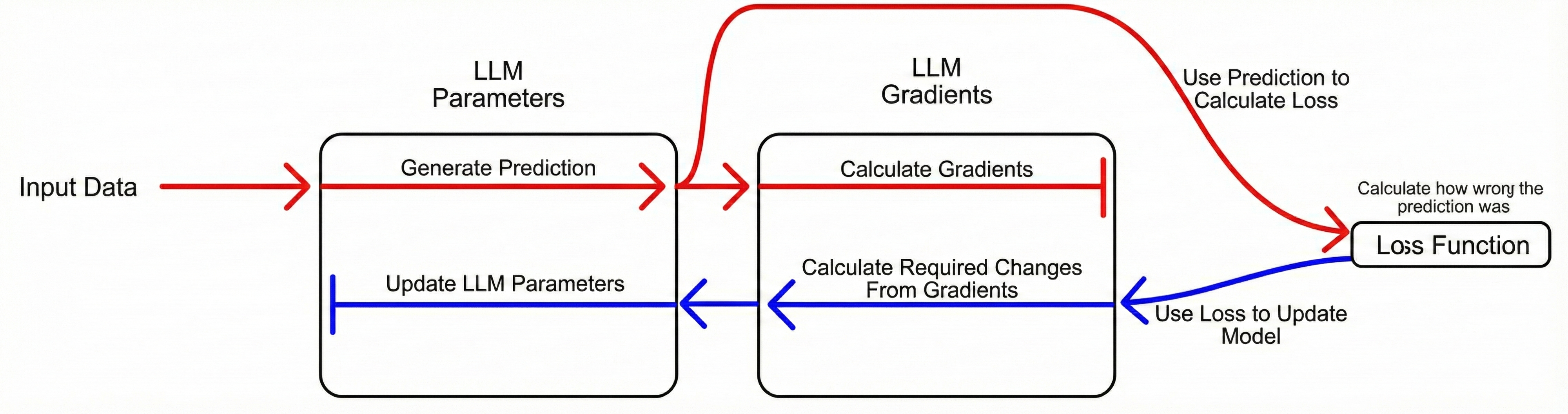
Since we are constrained by GPU memory, storing weights and gradients is a big issue. Checkpoints are usually also stored to save experiments, which are essentially copies of the model with different parameters. The result is that disk storage costs now explode. There is also the issue of transporting the data off the GPU, into RAM and then into storage, which adds more delays.

How to think about LoRA vs SFT

Instead of having the model make an inference and then update the parameters, the original parameters are "frozen" and we just have to learn how to make the changes that make it better at that specific task.

LoRA is able to leverage the following matrix properties:

1. Linear Independence

Linearly independent vectors contain different information compared to linearly dependent vectors which contain duplicate information.

2. Rank

The idea of rank is to quantify the amount of linear independence within a matrix. When a matrix is broken down into some number of linearly independent vectors, it is called reduced row echelon form. Now you can use the number of linearly independent vectors to describe the original matrix, which gives us its rank.

3. Matrix Factors

We can reduce a 2D matrix into a multiplication of two 1D vectors. Thus, if you have a large matrix with a high degree of linear dependence (and low rank), then that matrix can be expressed as a factor of two comparatively small matrices. This compaction is what allows LoRA to occupy such a small memory footprint.

Interestingly, LoRA describes tuning as not adjusting parameters but as learning parameter changes. The core assumption here is that LLMs have a lot of linear dependence as a result of having more parameters than required. Over parameterization has shown to be beneficial in pre-training. By taking advantage of dense layers' low intrinsic rank, it is possible to optimize the rank decomposition matrices instead, which reduces the number of parameters being trained.

Again, the key idea here is that we save the memory overhead and also time to recompute the entire model parameters every time.

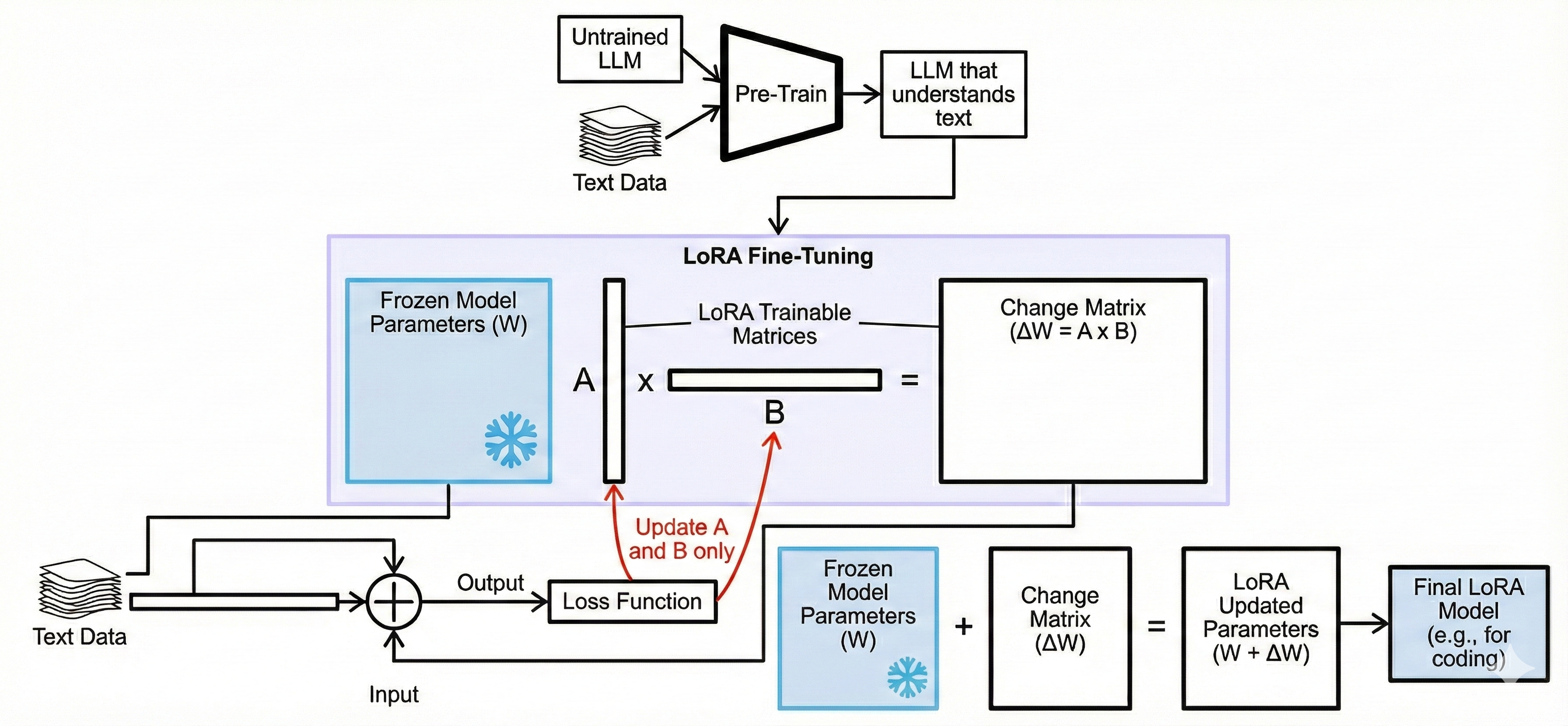
From the frozen model parameters, two matrices are created. Matrices A and B are used to create the change matrix. The frozen parameters and the change matrix are used to create output and then fed into the loss function. Then only matrices A and B are fine-tuned, and then the function is run again.

When we want to make inferences with the fine-tuned model, the change matrix is just recomputed and then used to change the weights, which creates the fine-tuned model.

Matrix depth

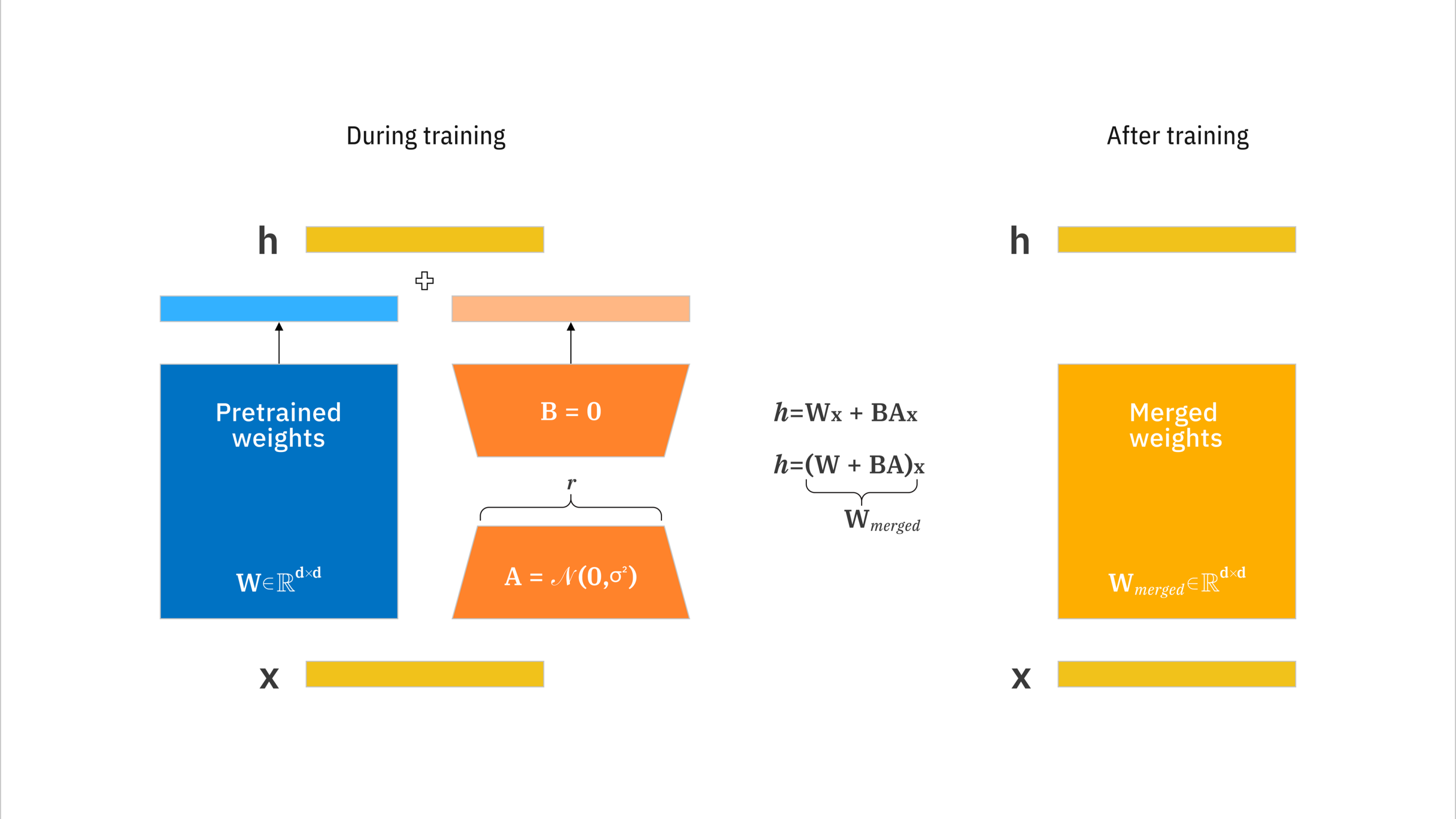
The LoRA paper talks about the r hyperparameter. Higher r values mean large A and B matrices and more linearly independent data is encoded. Obviously, they will consume a larger memory footprint. Interestingly, even low rank model parameters performed well. General advice is that if the data for fine-tuning is similar to pre-training, then a low r value is sufficient.

Applications

LoRA has found widespread adoption in:

• LLMs: Fine-tuning models like Llama, GPT, and Mistral for specific domains or instruction following.
• Stable Diffusion: Creating personalized image generation models that understand specific styles, characters, or concepts without retraining the entire UNet.

LoRA makes the power of state-of-the-art AI accessible to researchers and developers with limited hardware, democratizing the ability to customize foundation models.

References

• LoRA: Low-Rank Adaptation of Large Language Models
• LoRA: Intuitively and Exhaustively Explained